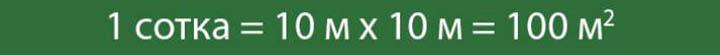Популярное
Полезные советы
Важно знать!
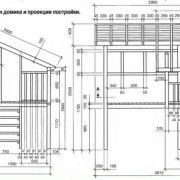
3 мастер-класса, как построить детский домик на участке
Виды детских домиков
«Двухуровневый дом – предел мечтаний»
Сложность и тип конструкции дачного развлекательного центра будет зависеть от буйства детской фантазии. Архитектура домика может быть любой....
Читать далее
5 марок лучших сигарет до 150 рублей, в которые до сих пор набивают настоящий табак
7 бытовых лайфхаков, которые сделают вашу жизнь проще
6 преимуществ и 5 недостатков разведения бычков на мясо
10 лучших сортов сладкого перца для теплиц
8 способов быстро и вкусно засолить селёдку
48 красивых сортов роз розового цвета с названиями и фото
18 вкусных салатов из свежей моркови
10 способов отличить настоящий мед от подделки
10 шагов как выращивать пекинскую капусту в открытом грунте
Рекомендуем
Лучшее

Важно знать!
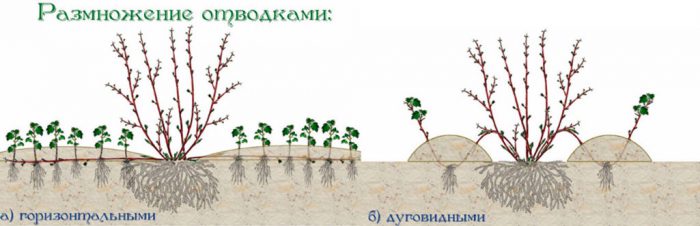
6 способов размножить орхидеи в домашних условиях
Размножения орхидеи Фаленопсис детками
Отсаживание «детки» – самый распространённый способ размножения Фаленопсиса. «Отпрыск» отделяется от материнского растения через 1,5–2 месяца после цветения....
Читать далее
20 вкусных салатов с сельдереем, которые стоит приготовить
5 самых распространенных бактериальных болезней растений
20 лучших обогревателей для дачи
9 поводов влюбиться в орхидею мильтонию и уход в домашних условиях
17 лучших садовых опрыскивателей
20 лучших сортов ремонтантной клубники
20 салатов с фасолью, которые стоит приготовить прямо сейчас
15 рецептов, как приготовить вкуснейший лимонный пирог
12 пошаговых рецептов вкусного тыквенного супа
Обсуждаемое

Важно знать!
20 простых салатов с грибами, которые тебе точно понравятся
Салат с грибами и курицей «Лесная поляна»
Подборку мы с Вами начнём с не менее популярного рецепта. Будем готовить салат под названием «Лесная поляна», многие называют его грибной
Думаю это не столь...
Читать далее
10 лучших рецептов виски в домашних условиях
10 самых полезных орехов
20 рецептов вкусных и полезных салатов со шпинатом
10 лучших сортов абрикос
13 способов использовать алоэ для здоровья и красоты
11 вечнозеленых растений, которые украшают сад круглый год
15 интересных фактов о ежах
70+ идей грядок на даче: красивые, «умные», «ленивые»
15 лучших рецептов картошки с грибами в духовке
Популярное
Актуальное

Важно знать!
6 правил выращивания сансевьеры в домашних условиях
Болезни и вредители
Если сансевиерия ханни содержится в мало-мальски подходящих условиях, она практически не страдает от болезней и вредителей.
Однако, не получая должного, вовсе не сложного, ухода, прежде...
Читать далее
5 секретов восстановления хрящевой ткани в колене
5 вариантов изготовления компостной ямы своими руками: фото, видео, подробные инструкции
20 отличных салатов с ветчиной на любой вкус и бюджет
5 рецептов бездрожжевого теста на воде, молоке, кефире и сметане
25 красивых цветочных картин для вдохновения
10 удивительных фактов о пальмах
7 самых дорогих цветов в мире
21 лучший рецепт приготовления заготовок с калиной на зиму в домашних условиях
5 способов размножения лилий
Обновления
 Статьи
Эстетика сада: Ландшафтный дизайн с хвойными растениями для фазенды
Статьи
Эстетика сада: Ландшафтный дизайн с хвойными растениями для фазенды
Хвойные растения в ландшафтном дизайне фазенд: творчество и экология для эстетического оазиса природы
В...
 Цветы
Посадка и уход за розами саженцами: секреты успешного разведения
Цветы
Посадка и уход за розами саженцами: секреты успешного разведения
Розы саженцами: посадка и уход - советы от профессионалов
Розы саженцами: посадка и уход
Красота розы...
 Статьи
Как взять небольшой займ до зарплаты?
Статьи
Как взять небольшой займ до зарплаты?
В наше непростое время иногда небольшая финансовая помощь может быть очень кстати. Для тех, кому нужен...
 Огород
50 фото разных видов и сортов снежноягодника, ? его полезные свойства и противопоказания
Огород
50 фото разных видов и сортов снежноягодника, ? его полезные свойства и противопоказания
Самый оригинальный сорт снежноягодника – Хенкок
Его часто выбирают, основываясь на фейковых фотографиях...
 Рецепты и заготовки
7 самых аппетитных рецептов вареников с картошкой и грибами
Рецепты и заготовки
7 самых аппетитных рецептов вареников с картошкой и грибами
Вареники картошкой: пошаговый рецепт
Это, можно, сказать классический вариант, так как начинка готовится...
 Рецепты и заготовки
15 самых вкусных рецептов приготовления айвы японской на зиму
Рецепты и заготовки
15 самых вкусных рецептов приготовления айвы японской на зиму
Айвовое варенье – рецепт приготовления с грецким орехом и лимонной цедрой
Считаю, что это лучший способ...
 10 советов про вылупление куриных яиц в инкубаторе
10 советов про вылупление куриных яиц в инкубаторе
Контроль работы инкубатора
Рассмотрим основные параметры работы инкубатора, которые нужно контролировать...
 Огород
15 лучших ранних сортов помидоров для открытого грунта
Огород
15 лучших ранних сортов помидоров для открытого грунта
Другие факторы
Окраска плодов
«Традиционный» цвет томатов – красный. Окраска плодов обусловлена наличием...
 Огород
7 самых красивых вьющихся цветов для сада
Огород
7 самых красивых вьющихся цветов для сада
Многолетние вьющиеся растения — для «ленивой» дачи
Многолетники — оптимальный выбор для тех, кто бывает...
 Огород
10 садовых хитростей для продвинутых дачников
Огород
10 садовых хитростей для продвинутых дачников
Полезные советы для дачи и огорода
1. Все растения любят отстоявшуюся теплую воду, лучше бочковую, где...
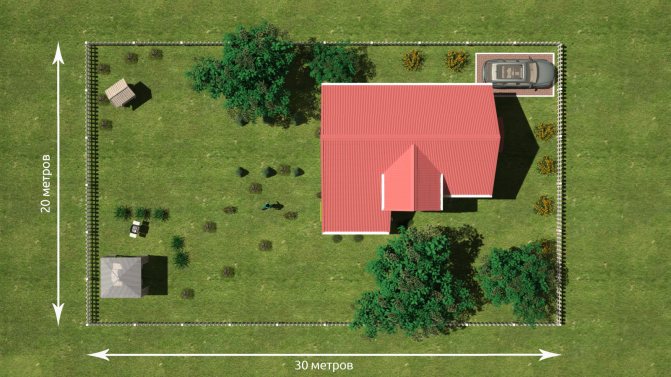 1 гектар это сколько соток земли
1 гектар это сколько соток земли
Сколько соток, квадратных метров, километров и аров в 1 га земли: таблица
Новое
Какая обувь модная...
 Рецепты и заготовки
10 рецептов соленых арбузов в банках на зиму
Рецепты и заготовки
10 рецептов соленых арбузов в банках на зиму
Бочки из пластика и нержавеющей стали
Пластмассовая бочка для закваски
Вместо деревянных бочек используются...